선형회귀의 목적

y가 x의 선형 함수로 표현될 수 있다고 가정하고, 독립 변수 x의 계수를 구하는 것← 새로운 입력값에 대한 출력을 얻기 위함.

이해를 돕기위해 아래와 같은 문제를 가정해보았습니다.
X: [1, 2 ,3]이라는 값들이 어떠한 필터를 거치면 Y: [4, 6, 8]이라는 형태로 바뀐다고 가정합니다.
Q: 이때 X=4일때 값은?

A: 10

우리는 이 10이라는 값이 f(x)=2x+2라는 함수를 거쳐나온 값이라는 것을 쉽게 유추할 수 있습니다.
데이터가 많다면 위와 같은 방법이 통할까요? 또한 데이터가 규칙적이지 않아 그나마 제일 근사하는 X를 찾아야한다면? 이 경우 사람이 연산하기 매우 힘들어집니다.

선형회귀란 사람이 추론하기 어려운 문제들에 대해서 주어진 데이터를 통해 이 f(x)를 찾는 방법론 중 하나라고 할 수 있습니다

\[f(x_i) = wx_i + b \quad \text{where} \quad f(x_i) \approx y_i\]

다만 현실에 존재하는 많은 데이터를 통해 예측값을 정확히 맞추는 함수 f(x)를 찾을 수 없기 때문에, 최대한 예측값에 근사하는 f(x)를 찾기 위해 노력해야 합니다.

↓보다 정확한 설명

선형 회귀 모델은 식으로 다음과 같이 나타낼 수 있습니다. y = Xw + b 여기서 y는 목표 변수, X는 입력 특성 행렬, w는 가중치 벡터, 그리고 b는 편향입니다. 위의 식은 입력 특성의 개수에 따라 2차원 공간에서 직선 또는 다차원 공간에서 초평면으로 나타나지는데 쉽게 이해하기위해 단변량이라고 한다면 y = Xw + b는 직선형태(y = xw + b)로 나타납니다. 구하려는 f(x)가 직선 xw+b라면 가중치는 기울기에 해당하며 편향은 y절편에 해당한다는 것을 알 수 있으며 가중치는 각 특성이 결과변수에 얼마나 영향을 미치는지를 결정하는 요소라는 것도 알 수 있습니다.



그럼 여기서 이 f(x)를 어떻게 찾지?
f(x)는 실제값 y와의 차이를 가능한 최대로 줄일 수 있는 함수를 구현할 수 있는가로부터 시작합니다.

최소제곱법

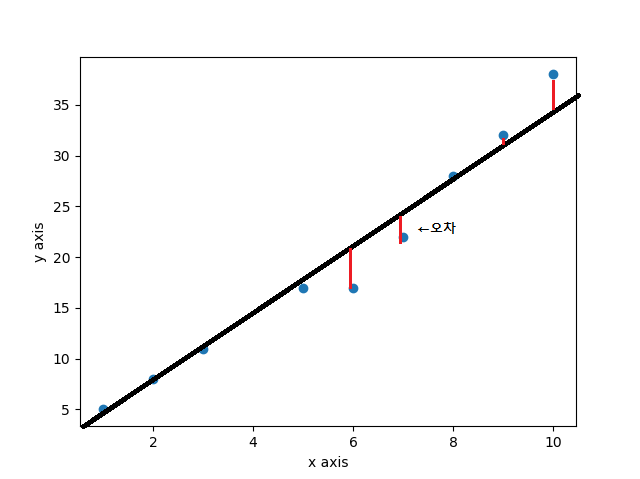
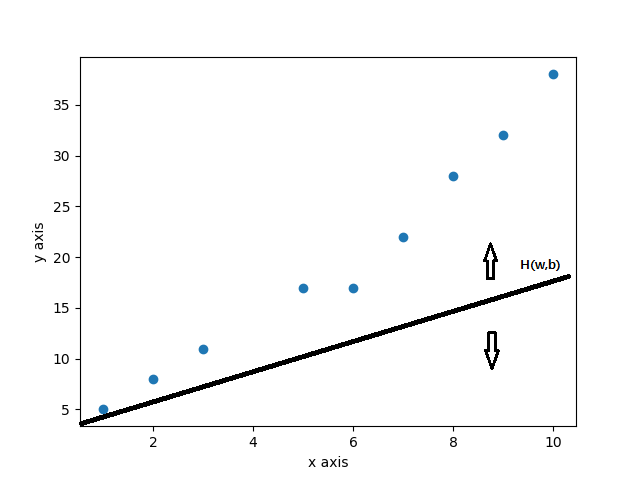
f(X)와 y의 차이를 어떻게 측정할 것인지에 따라서 달라질 수 도 있지만 일반적으로 회귀문제에서는 평균제곱오차(Mean Squared Error, MSE)라는 성능척도를 사용합니다.
\(loss function=\displaystyle\sum_{i=1}^{m}{(f(x_i)-y_i)^2}\)

MSE1 MSE2

그리고 이러한 손실함수를 최소화해주는 다양한 최적화 기법들이 존재하며 이중에는 대표적으로 경사하강법(Gradient Descent)이 존재합니다.

요약

  • 선형회귀는 주어진 데이터를 바탕으로 결과(종속 변수)과 예측값 사이의 차이를 최소화 하는 f(x)를 찾는 과정입니다.

  • f(x)는 독립 변수들과 관련된 선형 방정식으로 표현되며, 이를 통해 종속 변수를 예측할 수 있습니다.

  • 선형회귀에서는 오차의 제곱합을 최소화하는 방식으로 최적의 f(x)를 찾습니다.

결과적으로 선형회귀를 하기 위해서는 오차의 제곱합이라는 목적함수를 최소화해야하는 문제를 해결해야되는데 이를 위해 다양한 최적화방법(optimization method) 중 하나를 선택해야합니다.

경사하강법

최적화방법에는 여러가지가 있고 경사하강법 안에서도 여러가지가 존재합니다.

몇 가지의 최적화 방법들을 포함하여 가장 기본적인 경사하강법과 변형된 경사하강법들을 소개해보려고합니다.

정규방정식(Normal Equation)

선형회귀 문제의 해를 직접적으로 구하는 수학적 방법입니다. 이 방법은 행렬 연산을 이용하여 오차의 제곱합을 최소화하는 해를 계산합니다.
\(\theta=(X^T*X)^{-1}*X^T*y\)

여기서 theta는 파라미터 벡터, X는 특성 행렬, y는 결과값 벡터입니다.

import numpy as np

# 가상의 데이터 생성
X = np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 정규방정식을 이용한 선형회귀
X_b = np.c_[np.ones((100, 1)), X]  # bias 항 추가
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

print(theta_best) # [[3.86501051], [3.27832357]]

장점

  1. 계산복잡도가 낮기에 계산이 빠르며 정확한 파라미터 값을 구할 수 있습닌다.

  2. 정규방정식을 사용하면 특성 개수가 많아져도 성능이 유지됩니다.← 특성 간 상관관계가 낮을 때 한정

  3. 추가적인 모델 조정없이 바로 사용할 수 있습니다.

단점

  1. 역행렬을 계산해야하므로, 특성 개수가 많아질수록 계산 속도가 느려질 수 있습니다.

  2. 특성 간 상관관계가 높은 경우, 역행렬이 존재하지 않거나 계산이 불안정해질 수 있습니다.

2번에 대한 부가설명

입력 변수 간에 강한 상관관계가 있는 경우 발생하는 문제를 **다중공선성(multicollinearity)**이라고 함. 특정한 특성 간의 상관관계가 매우 높아진다면 행렬의 랭크가 줄어들게되는데 이는 곧 상관관계를 제대로 파악하지못한다면 역행렬을 알아내기가 매우 어렵다는 것과 같음. **랭크(rank): 행렬에서 선형 독립적인 행의 개수**


좌표하강법(Coordinate Descent)

한번에 하나의 파라미터만을 업데이터하면서 오차의 제곱합을 최소화하는 방향으로 진행하는 최적화 방법입니다. 좌표하강법은 일반적으로 Lasso, Ridge회귀와 같은 정규화가 있는 선형 회귀 모델에 주로 사용됩니다.

(파라미터를 각각의 축 방향으로 이동시켜가며, 그 때의 MSE를 계산하고 MSE를 최소화하는 파라미터 값을 찾는 방식)
\(\\theta\_j=(X\_j^T\*(y-X\*\\theta\_{except\_j}))/(X\_j^T\*X\_i)\)

  • X_j: j번째 특성(feature)에 대한 데이터(벡터)
  • θ_except_j: j번째 파라미터를 제외한 모든 파라미터의 값(벡터)
  • X: 전체 특성(feature)에 대한 데이터 행렬
  • y: 타겟 변수(target variable)에 대한 데이터(벡터)
import numpy as np

# 가상의 데이터 생성
X = np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 좌표하강법을 이용한 선형회귀
def coordinate_descent(X, y, iterations):
    m, n = X.shape
    X_b = np.c_[np.ones((m, 1)), X]
    theta = np.random.randn(n + 1, 1)

    for _ in range(iterations):
        for i in range(n + 1):
            theta[i] = (X_b[:, i].T.dot(y - X_b.dot(theta)) + theta[i] * X_b[:, i].T.dot(X_b[:, i])) / X_b[:, i].T.dot(X_b[:, i])
    return theta

theta_best = coordinate_descent(X, y, iterations=1000)

print(theta_best) #[[3.61219908], [3.73152664]]

장점

  1. 각 파라미터를 순차적으로 업데이트하기 때문에, 계산량이 적어서 속도가 빠릅니다.
  2. 각 파라미터를 독립적으로 업데이트하기 때문에, 다중회귀분석에서 변수의 개수가 많은 경우에도 적용이 가능합니다.
  3. 각 축 방향으로 순차적으로 이동하면서 MSE를 최소화하는 파라미터 값을 찾기 때문에, 이동경로가 좀 더 직관적이고 해석하기 쉽습니다.

단점

  1. 각 파라미터를 순차적으로 업데이트하기 때문에, 전역 최적값(global minimum)이 아닌 지역 최적값(local minimum)에 빠질 가능성이 있습니다.

  2. 비등방성(anisotropy)이 강한 함수에서는 수렴 속도가 매우 느려질 수 있습니다.

(강한 비등방성: 함수의 기울기가 방향에 따라 급격한 차이를 보이는 것)

  1. 순차적으로 최적화를 수행하므로, 병렬화가 어렵습니다.
  2. 함수가 미분 가능하지 않은 경우에는 적용하기 어려울 수 있습니다.


경사하강법(Gradient Descent)

↑이 글에서 자세하게 다루어볼 최적화방법
\(θ = θ - η \* ∇J(θ)\)

  • θ는 매개변수 벡터
  • η는 학습률
  • m은 데이터셋의 크기
  • X_i는 i번째 데이터 포인트
  • y_i는 i번째 데이터 포인트

즉, 경사하강법이란 미분을 통해 손실함수의 기울기를 구하고 업데이트를 하면서 기울기가 0인 지점(극값)을 찾아 손실함수의 최소값을 구하는 과정을 말합니다.

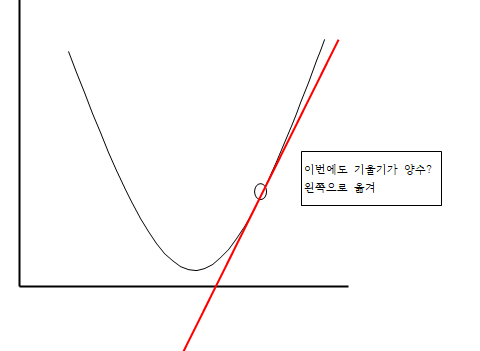
이해하기 쉽게 간단하게 이미지로 시각화를 해보았습니다. 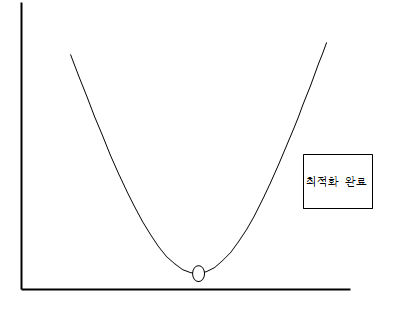GD1 GD2 GD3 만약 이동간격을 크게한다면 어떻게 될까요? GD4
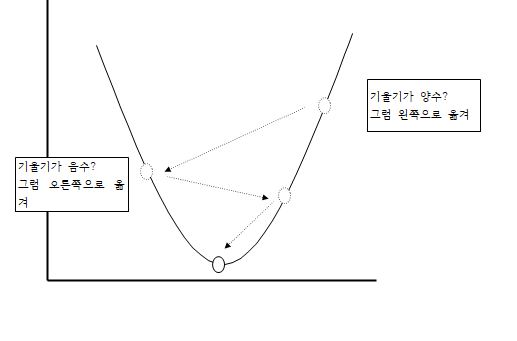
위에서 말한 이동간격을 경사하강법에서는 학습률(learning late)이라고 표현합니다.

이를 작게한다면 아래와 같이 극값에 이르지 못하고 한 공간에 머무르게 되는 문제가 발생하는데 이를 지역최적화(Local Minima)라고 합니다. 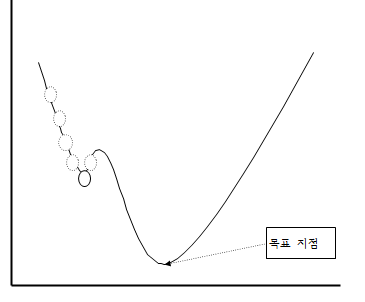GD5 반대로 학습률을 너무 크게 한다면 극값에 수렴하지못하고 크게 벗어나게 될 가능성이 존재합니다.

import numpy as np
​
# 가상의 데이터 생성
X = np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
​
# 경사 하강법을 이용한 선형회귀
def gradient_descent(X, y, learning_rate, iterations):
    m = len(y)
    theta = np.random.randn(2, 1)
    X_b = np.c_[np.ones((m, 1)), X]
​
    for _ in range(iterations):
        gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
        theta -= learning_rate * gradients
    return theta
​
theta_best = gradient_descent(X, y, learning_rate=0.1, iterations=1000)
​
print(theta_best) # [[3.92026167] [2.92196034]]

장점

  1. 일반적으로 다양한 최적화 문제에 적용할 수 있어 활용도가 높습니다.
  2. 방향성이 있어, 전역 최적해(global minimum)에 빠르게 수렴할 가능성이 높습니다.
  3. 속도와 정확도를 조절하는 학습률(learning rate) 파라미터를 통해 알고리즘의 성능을 조절할 수 있습니다.

단점

  1. 기울기가 매우 작거나 0인 경우에는 수렴 속도가 느려질 수 있습니다.
  2. 초기값에 따라서 지역 최적해(local minimum)에 갇히거나 최적해를 찾지 못할 수도 있습니다.
  3. 학습률(learning rate) 파라미터의 선택이 중요하며, 잘못 설정하면 발산할 수도 있습니다.

일반적으로 많은 task에서는 경사하강법을 이용하여 최적화를 진행합니다.

위에서 한번 언급했지만 경사하강법 안에서도 여러가지 경사하강법들이 존재하는데요.

아래의 글에서 대표적인 경사하강법들을 추가로 알아보려고 합니다.

배치 경사 하강법 (Batch Gradient Descent)

\(θ = θ - η \* (1/m) \* Σ(X\_i \* (X\_i \* θ - y\_i))\)

전체 데이터셋을 사용하여 매개변수를 업데이트하며 상대적으로 정확하지만 대규모 데이터셋에는 시간이 오래 걸릴 수 있습니다.

장점: 전체 데이터셋을 사용하기 때문에 안정적인 수렴합니다.
단점: 대규모 데이터셋에서 시간이 오래 걸립니다.

확률적 경사 하강법 (Stochastic Gradient Descent, SGD)

\(θ = θ - η \* (X\_j \* (X\_j \* θ - y\_j))\)

매개변수를 업데이트할 때 무작위로 선택한 단일 데이터 포인트를 사용합니다. 더 빠르긴하지만, 더 불안정하고 최적해로 수렴하는 과정이 불규칙하게 진행됩니다. 그러나 이러한 불규칙성 때문에 지역 최적해(local optima)를 벗어나는 데 도움이 됩니다.

장점: 계산빠르며 지역 최적해를 벗어날 수 있습니다.
단점: 최적해에 도달할 때까지의 과정이 불규칙합니다.

미니 배치 경사 하강법(Mini-batch Gradient Descent)

\(θ = θ - η \* (1/|B|) \* Σ(X\_k \* (X\_k \* θ - y\_k))\)

데이터셋의 작은 부분(미니 배치)을 사용하여 매개변수를 업데이트합니다. 이 방법은 배치 경사 하강법과 확률적 경사 하강법의 중간 정도의 성능을 가집니다. 이 방법은 일반적으로 더 안정적이고 빠르게 수렴하는 경향이 있습니다

장점: 계산이빠르며 안정적으로 수렴합니다.
단점: 최적의 배치 크기를 선택해야 합니다.

전체 코드 구현

import numpy as np

# 가상의 데이터 생성
X = np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

def gradient_descent(X, y, learning_rate, iterations, method, batch_size=None):
    m = len(y)
    theta = np.random.randn(2, 1)
    X_b = np.c_[np.ones((m, 1)), X]

    if method == "batch":
        for _ in range(iterations):
            gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
            theta -= learning_rate * gradients

    elif method == "sgd":
        for _ in range(iterations):
            random_idx = np.random.randint(m)
            xi = X_b[random_idx:random_idx+1]
            yi = y[random_idx:random_idx+1]
            gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
            theta -= learning_rate * gradients

    elif method == "mini_batch":
        if batch_size is None:
            raise ValueError("적합한 배치 크기를 지정하세요.")
        for _ in range(iterations):
            random_indices = np.random.randint(0, m, batch_size)
            X_b_mini = X_b[random_indices]
            y_mini = y[random_indices]
            gradients = 2/batch_size * X_b_mini.T.dot(X_b_mini.dot(theta) - y_mini)
            theta -= learning_rate * gradients

    return theta

# 배치 경사 하강법
theta_best_batch = gradient_descent(X, y, learning_rate=0.1, iterations=1000, method="batch")
print("Batch Gradient Descent:", theta_best_batch)

# 확률적 경사 하강법
theta_best_sgd = gradient_descent(X, y, learning_rate=0.1, iterations=1000, method="sgd")
print("Stochastic Gradient Descent:", theta_best_sgd)

# 미니 배치 경사 하강법
theta_best_mini_batch = gradient_descent(X, y, learning_rate=0.1, iterations=1000, method="mini_batch", batch_size=20)
print("Mini-batch Gradient Descent:", theta_best_mini_batch)

출력 결과

Batch Gradient Descent: [[4.06759234], [3.30899451]]
Stochastic Gradient Descent: [[3.60920537], [3.20428641]]
Mini-batch Gradient Descent: [[3.93573628], [3.21683228]]

위에서 설명한 경사하강법 말고도 모멘텀 경사 하강법, AdaGrad, RMSProp, Adam, Nadam과 같은 경사하강법이 존재합니다.